Impulse-based dynamic simulation library (IBDS)
-
Dirk Gregorius
- Posts: 861
- Joined: Sun Jul 03, 2005 4:06 pm
- Location: Kirkland, WA
The problem (as you will propably soon encounter if people start using your engine) that they are simply not aware of those kind of stuff, e.g. they don't know what a stiff system is. At this point you need make compromises and one could argue that a general win in stability due to e.g. Symplectic Euler at a cost of some tiny loss in precision might be a good deal.
-
raigan2
- Posts: 197
- Joined: Sat Aug 19, 2006 11:52 pm
-
Erin Catto
- Posts: 316
- Joined: Fri Jul 01, 2005 5:29 am
- Location: Irvine
Yes, the integrator matters. Some integrators are better than others. Explicit Euler is the worst integrator and the parabolic integrator is not much better.
The parabolic integrator is only exact if the forces are constant for _all time_. Unfortunately, constraint forces are not in that category. So when you use the parabolic integrator to simulate joints, the results are hardly better than explicit Euler.
The parabolic integrator is only exact if the forces are constant for _all time_. Unfortunately, constraint forces are not in that category. So when you use the parabolic integrator to simulate joints, the results are hardly better than explicit Euler.
-
Jan Bender
- Posts: 111
- Joined: Fri Sep 08, 2006 1:26 pm
- Location: Germany
You are right. Using my method it doesn't matter which integrator you use to determine the future state. Of course you have to use the same integrator for the prediction and for the time step.raigan2 wrote: Does the integration method matter? My understanding was that you could use whatever integrator you prefer to generate the future states.
For the parabolic integrator the forces have just to be constant for the time interval of one time step (since you integrate over this interval). Okay, I see there is a misunderstanding. I DON'T compute constraint forces. Otherwise I would have the problem with the integrator. I just use impulses and apply them directly (no integration of the impulses). So in the end I don't have to solve difficult differential equations (my boss always say that this is the main advantage of our method), I just have to integrate the equations for the center of mass, the linear velocity, the angular velocity and the quaternion. In none of these equations internal continuous forces occur. So the equations for linear velocity and the center of mass can be directly solved by:Erin Catto wrote:Yes, the integrator matters. Some integrators are better than others. Explicit Euler is the worst integrator and the parabolic integrator is not much better.
The parabolic integrator is only exact if the forces are constant for _all time_. Unfortunately, constraint forces are not in that category. So when you use the parabolic integrator to simulate joints, the results are hardly better than explicit Euler.
v(t+dt) = v(t) + Fext/m * dt
c(t+dt) = c(t) + v(t)*dt + 1/2 * Fext/m * t^2
(if the external forces Fext are constant for the time interval dt).
The equations for angular velocity and the quaternion have to be solved by integration. I use a Runge-Kutta method of fourth order to do this.
I hope that makes the thing a bit clearer.
Jan
-
Erin Catto
- Posts: 316
- Joined: Fri Jul 01, 2005 5:29 am
- Location: Irvine
I mispoke slightly. The parabolic integrator does not give exact results for forces that vary with position or velocity. The force can vary with time, but should never vary during the time step. So basically, you can have a stepped force function that does not depend on position or velocity.
Now in terms of impulse simulation, the impulses do vary with position and velocity. This makes sense because we expect the reaction forces in a robot arm to vary depending on the arm's joint angles and velocities.
Recall that an impulse is just the integral of a force. So when you apply impulses to solve constraints, you are implicitly integrating a force. And what integrator are you using to integrate that force? Well it is just a forward Euler:
v[t+h] = v[t] + constraint_impulse = v[t] + h * constraint_force
So let's mix this with the parabolic integrator and consider a system only composed of particles (no rotations):
p[t+h] = p[t] + h * v[t] + 0.5 * h^2 * a
v1[t+h] = v[t] + h * a
v2[t+h] = v1[t+h] + h * constraint_force
Now this system may vary slightly from Jan's, but it should be sufficient to make my point.
So what is the accuracy of the position? If you have no constraints and only gravity, the position result is exact. More precisely, the integrator is exact to O(h^2).
Now lets add constraints. Assume you can compute the constraint impulse exactly. Because you have a constraint impulse that likely varies with position and velocity, the integrator now only O(h) accurate. So the O(h^2) accuracy of the parabolic integrator is nullified by the O(h) accuracy of the constraint integration. In other words, you no longer have any predictable benefit from the parabolic position integrator.
Now in terms of impulse simulation, the impulses do vary with position and velocity. This makes sense because we expect the reaction forces in a robot arm to vary depending on the arm's joint angles and velocities.
Recall that an impulse is just the integral of a force. So when you apply impulses to solve constraints, you are implicitly integrating a force. And what integrator are you using to integrate that force? Well it is just a forward Euler:
v[t+h] = v[t] + constraint_impulse = v[t] + h * constraint_force
So let's mix this with the parabolic integrator and consider a system only composed of particles (no rotations):
p[t+h] = p[t] + h * v[t] + 0.5 * h^2 * a
v1[t+h] = v[t] + h * a
v2[t+h] = v1[t+h] + h * constraint_force
Now this system may vary slightly from Jan's, but it should be sufficient to make my point.
So what is the accuracy of the position? If you have no constraints and only gravity, the position result is exact. More precisely, the integrator is exact to O(h^2).
Now lets add constraints. Assume you can compute the constraint impulse exactly. Because you have a constraint impulse that likely varies with position and velocity, the integrator now only O(h) accurate. So the O(h^2) accuracy of the parabolic integrator is nullified by the O(h) accuracy of the constraint integration. In other words, you no longer have any predictable benefit from the parabolic position integrator.
-
Jan Bender
- Posts: 111
- Joined: Fri Sep 08, 2006 1:26 pm
- Location: Germany
Correct. Since I just have external forces in the equations this is no problem except if you want to simulate springs very accurately. Otherwise you usually have just gravity.I mispoke slightly. The parabolic integrator does not give exact results for forces that vary with position or velocity. The force can vary with time, but should never vary during the time step. So basically, you can have a stepped force function that does not depend on position or velocity.
My impulse-based method works different as I already mentioned. The impulses don't occur in the equations that have to be integrated as variable.Now in terms of impulse simulation, the impulses do vary with position and velocity. This makes sense because we expect the reaction forces in a robot arm to vary depending on the arm's joint angles and velocities.
That's wrong. I don't compute the impulses by a forward Euler. The impulses are determined by using the prediction of the error that occurs if the joint points have a ballistic motion. Then the impulses are applied to the joint points at the actual point of time. That means the velocities changes instantaneous. So v(t) is changed directly and the impulse doesn't have to be regarded during the integration.Recall that an impulse is just the integral of a force. So when you apply impulses to solve constraints, you are implicitly integrating a force. And what integrator are you using to integrate that force? Well it is just a forward Euler:
v[t+h] = v[t] + constraint_impulse = v[t] + h * constraint_force
That is wrong. It is absolutely exact. You probably know Taylor series (http://en.wikipedia.org/wiki/Taylor_series). Since gravity is the only force the acceleration is constant:So what is the accuracy of the position? If you have no constraints and only gravity, the position result is exact. More precisely, the integrator is exact to O(h^2).
a=g=9.81
d/dt v = v' = a
d/dt p = p' = v
The Taylor series says:
p(t+h) = p(t) + p'(t) * h + 1/2 * p''(t) * h^2 + 1/6 * p'''(t) * h^3 + ...
Since p'''=v''=a'=0 (a is constant), the exact result is
p(t+h) = p(t) + p'(t) * h + 1/2 * p''(t) * h^2 = p(t) + v(t)*h + 1/2*a*h^2
In this case the equation is NOT only exact to O(h^2).
That is also wrong since the impulses are computed in a different way. They are determined for the time t and applied at time t. No variation during the time step has to be regarded. The impulse is chosen at time t so that at time t+h the positions are corrected. If you want to know more about the numerical error of my method you should read "Impulse-Based Dynamic Simulation of Higher Order and Numerical Results". In this report is also described how an accuracy of O(h^10) or even higher can be achieved (of course the simulation gets slower if you want to have higher accuracy).Now lets add constraints. Assume you can compute the constraint impulse exactly. Because you have a constraint impulse that likely varies with position and velocity, the integrator now only O(h) accurate. So the O(h^2) accuracy of the parabolic integrator is nullified by the O(h) accuracy of the constraint integration. In other words, you no longer have any predictable benefit from the parabolic position integrator.
I hope that makes a few things clearer.
Jan
-
Erin Catto
- Posts: 316
- Joined: Fri Jul 01, 2005 5:29 am
- Location: Irvine
My formula says nothing about how the impulse is computed, only how it affects the velocity. Do you not apply an impulse to adjust the velocity at a single point of time in the time step?That's wrong. I don't compute the impulses by a forward Euler. The impulses are determined by using the prediction of the error that occurs if the joint points have a ballistic motion. Then the impulses are applied to the joint points at the actual point of time. That means the velocities changes instantaneous. So v(t) is changed directly and the impulse doesn't have to be regarded during the integration.
The parabolic integrator is accurate to O(h^2). With a constant force, that is enough to give an exact solution. Obviously the parabolic integrator is not infinitely exact for any force, so it must have a certain order of approximation of the Taylor series, just like all integrators do. Examples:
Explicit Euler: O(h)
Backwards Euler: O(h)
Symplectic Euler: O(h)
Parabolic: O(h^2) for constant force
Midpoint: O(h^2)
4th Order Runge-Kutta: O(h^4)
What you wrote is O(h^2), so you are not showing that the integrator is accurate _beyond_ O(h^2), only that the acceleration in your particular case is constant.p(t+h) = p(t) + p'(t) * h + 1/2 * p''(t) * h^2 = p(t) + v(t)*h + 1/2*a*h^2
In this case the equation is NOT only exact to O(h^2).
Here's a numerical experiment:
- Derive the equations of motion for a rigid body pendulum using the joint angle theta.
- Simulate the equation (a single ODE in theta) using RK4 with a very small time step. Call the result theta_exact.
- Now simulate the same pendulum using your impulse method.
- Use time steps like this: 1/2, 1/8, 1/16, 1/32, ...
- Measure the error between your simulations and theta_exact.
- Plot the error vs the time step size. On a log plot the slope will give you the order of accuracy.
I looked at that paper and on the front page is says: "It turned out that the impulseThat is also wrong since the impulses are computed in a different way. They are determined for the time t and applied at time t. No variation during the time step has to be regarded. The impulse is chosen at time t so that at time t+h the positions are corrected. If you want to know more about the numerical error of my method you should read "Impulse-Based Dynamic Simulation of Higher Order and Numerical Results". In this report is also described how an accuracy of O(h^10) or even higher can be achieved (of course the simulation gets slower if you want to have higher accuracy).
methods of higher integration order are all of O(h3)" Why are you saying that the accuracy is up to O(h^10)?
In the end perhaps your impulse method has higher accuracy for constant forces. My main objection is to putting out a method to game developers that will fall apart as soon as any springs are introduced. It is fine to give such a method to engineers and academics for research because they are equipped to understand the caveats. But should we not prefer a small drop in accuracy for a much more robust solution?
-
Jan Bender
- Posts: 111
- Joined: Fri Sep 08, 2006 1:26 pm
- Location: Germany
I just apply impulses at a time t0 (the beginning of the time step) and this is enough for the time step.My formula says nothing about how the impulse is computed, only how it affects the velocity. Do you not apply an impulse to adjust the velocity at a single point of time in the time step?
Taylor's theorem says the following:What you wrote is O(h^2), so you are not showing that the integrator is accurate _beyond_ O(h^2), only that the acceleration in your particular case is constant.

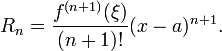
In the parabolic integrator we have R_2. In general this leads to an error or O((x-a)^3) = O(h^3). In my case the force is constant and so f'' is constant which means that f'''=0. So the term R_2=0 and this means that in this special case the error is 0.
Do you agree with me that this integrator determines a exact result if only constant forces act and no constraint is given? If you don't agree with this, then please give me a proof or explain to me why you say that it is only accurate to O(h^2) because I don't understand your point. And if it is only accurate to O(h^2) what do you think is the exact solution of e.g. a simulation of particle falling down?
This example contains a constraint and until now I was speaking of a model without constraints.Here's a numerical experiment:
The problem of the methods of higher integration order is that it works in theory (we were able to proof that a higher integration order is possible) but we had never the time to completely implement the stuff correctlyI looked at that paper and on the front page is says: "It turned out that the impulse
methods of higher integration order are all of O(h3)" Why are you saying that the accuracy is up to O(h^10)?
You are right. For my thesis spring forces were not very important since they are well-known. I will implement the following for my simulator. If a model contains rigid bodies with spring forces or other continuous forces then a Runge-Kutta of fourth order will be used to integrate the positions and velocities. This should work better or what do you think?In the end perhaps your impulse method has higher accuracy for constant forces. My main objection is to putting out a method to game developers that will fall apart as soon as any springs are introduced. It is fine to give such a method to engineers and academics for research because they are equipped to understand the caveats. But should we not prefer a small drop in accuracy for a much more robust solution?
Jan
-
Erin Catto
- Posts: 316
- Joined: Fri Jul 01, 2005 5:29 am
- Location: Irvine
I agree. I think we are just having a terminology problem. When I say "accurate to O(h^2)", that means the error is O(h^3).Do you agree with me that this integrator determines a exact result if only constant forces act and no constraint is given? If you don't agree with this, then please give me a proof or explain to me why you say that it is only accurate to O(h^2) because I don't understand your point. And if it is only accurate to O(h^2) what do you think is the exact solution of e.g. a simulation of particle falling down?
For games I wouldn't bother with RK4. Take a look at "Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations" by Hairer, et al. The book shows why symplectic Euler is such a great method. Best of all, it is very inexpensive to implement.
-
Jan Bender
- Posts: 111
- Joined: Fri Sep 08, 2006 1:26 pm
- Location: Germany
Yes, I know. But I meant that in this special case the error term R is exactly 0 and not of O(h^3). Can you tell me why you think it is O(h^3) where this h^3 should come from.I agree. I think we are just having a terminology problem. When I say "accurate to O(h^2)", that means the error is O(h^3).
At the moment you can choose between RK4 and Taylor of any order in my simulator. I think I will give the user some more integrators to choose.For games I wouldn't bother with RK4. Take a look at "Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations" by Hairer, et al. The book shows why symplectic Euler is such a great method. Best of all, it is very inexpensive to implement.
Jan
-
Erin Catto
- Posts: 316
- Joined: Fri Jul 01, 2005 5:29 am
- Location: Irvine
I'll try to say the same thing again in a different way:
The parabolic integrator has O(h^3) error. In the case of constant acceleration the coefficients of all terms O(h^3) and higher are zero. When you have constraints the acceleration is generally not constant, therefore the coefficients of O(h^3) and higher terms are not zero. When you have undamped springs, the parabolic integrator is unstable (just like explicit Euler).
The parabolic integrator has O(h^3) error. In the case of constant acceleration the coefficients of all terms O(h^3) and higher are zero. When you have constraints the acceleration is generally not constant, therefore the coefficients of O(h^3) and higher terms are not zero. When you have undamped springs, the parabolic integrator is unstable (just like explicit Euler).
-
Jan Bender
- Posts: 111
- Joined: Fri Sep 08, 2006 1:26 pm
- Location: Germany
Okay, if you have constraints or springs you will have an error of O(h^3). But for constant external forces, no springs and no constraints the acceleration is constant and the p'''=v''=a'=0, so the coefficients of O(h^3) and higher terms are 0. Can you agree with this?The parabolic integrator has O(h^3) error. In the case of constant acceleration the coefficients of all terms O(h^3) and higher are zero. When you have constraints the acceleration is generally not constant, therefore the coefficients of O(h^3) and higher terms are not zero. When you have undamped springs, the parabolic integrator is unstable (just like explicit Euler).
Jan
-
Erin Catto
- Posts: 316
- Joined: Fri Jul 01, 2005 5:29 am
- Location: Irvine
-
Jan Bender
- Posts: 111
- Joined: Fri Sep 08, 2006 1:26 pm
- Location: Germany
-
Erin Catto
- Posts: 316
- Joined: Fri Jul 01, 2005 5:29 am
- Location: Irvine
That is true if v = dp/dt, but v is modified by impulses.
In the higher-order integration paper you guys discussed the error of imp2-imp11, but I'm guessing the one you are proprosing for games is imp1? Did you guys perform the numerical experiment to measure the error of imp1?
Also, what about your rotation integration? Does it have O(h^3) error?
In the higher-order integration paper you guys discussed the error of imp2-imp11, but I'm guessing the one you are proprosing for games is imp1? Did you guys perform the numerical experiment to measure the error of imp1?
Also, what about your rotation integration? Does it have O(h^3) error?